Slope, a fundamental concept in mathematics, plays a pivotal role in various fields, including geometry, physics, and engineering. This guide delves into the intricacies of slope, exploring its definition, geometric interpretation, and practical applications.
In geometry, slope represents the angle of inclination of a line, providing insights into its steepness. It serves as a key factor in determining the rate of change, which finds applications in describing the steepness of roads, calculating the gradient of rivers, and analyzing the growth or decay of various phenomena.
Definition and Mathematical Representation
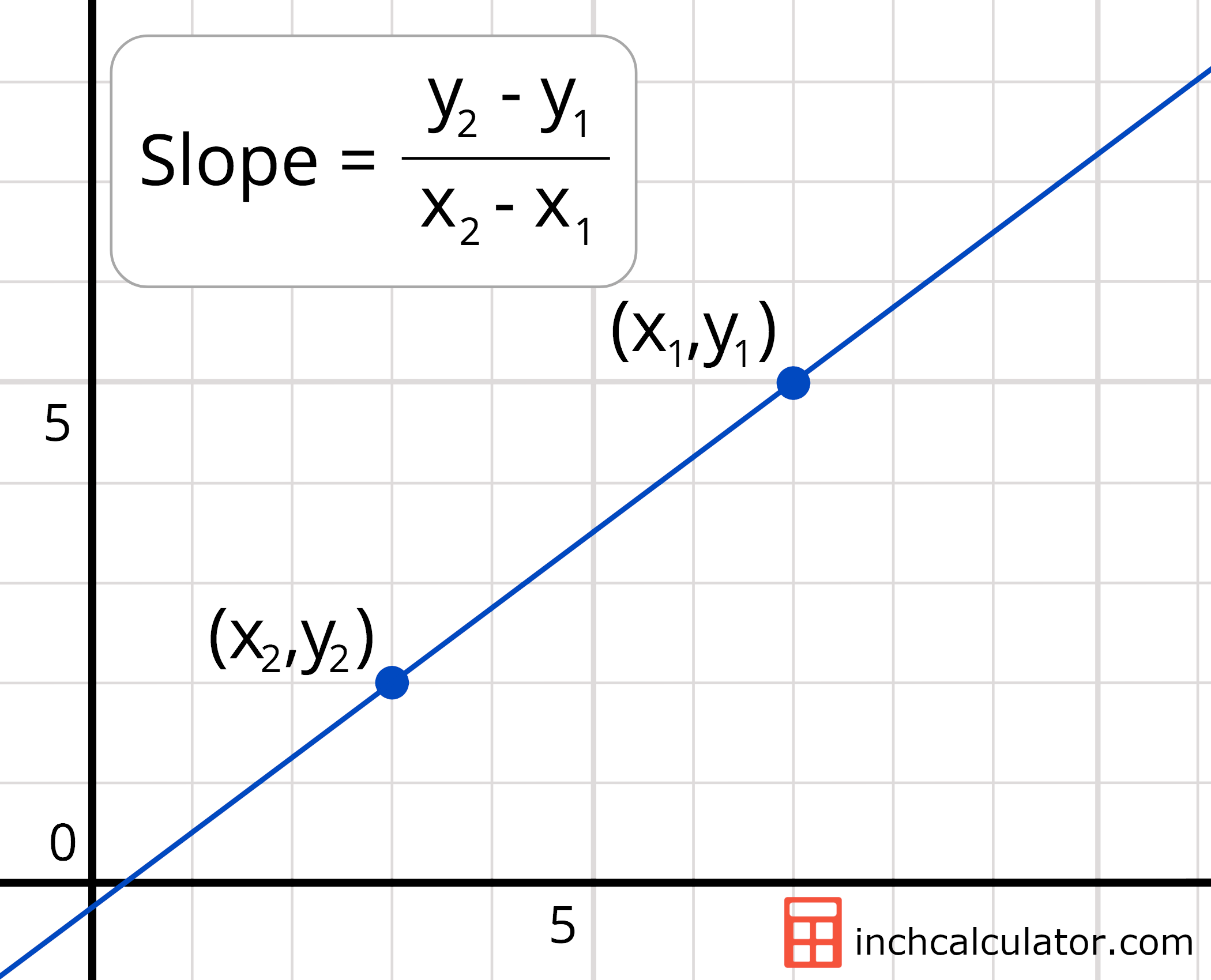
In mathematics, slope refers to the steepness or inclination of a line. It quantifies the rate of change in the y-coordinate with respect to the x-coordinate.
The mathematical formula for calculating slope is:
m = (y2 – y1) / (x2 – x1)
where (x1, y1) and (x2, y2) are any two distinct points on the line.
Relationship between Slope and Rate of Change
Slope represents the rate of change in the y-coordinate for a unit change in the x-coordinate. For instance, if a line has a slope of 2, it means that for every 1 unit increase in the x-coordinate, the y-coordinate increases by 2 units.
Geometric Interpretation
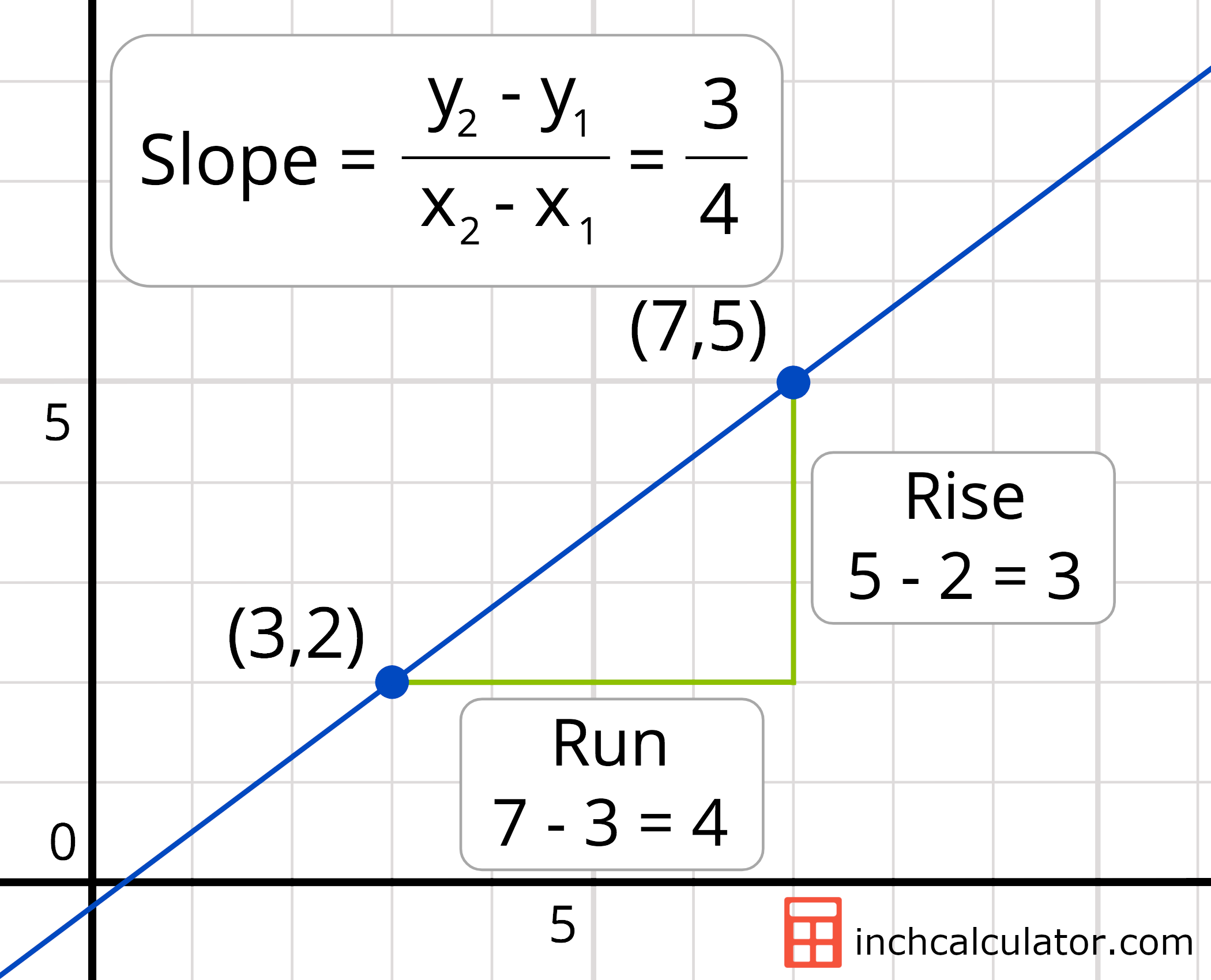
Geometrically, slope represents the ratio of the vertical change (rise) to the horizontal change (run) along a line. It measures the steepness of the line.
Steepness of a Line
A line with a positive slope slants upward from left to right, indicating a positive rate of change. A negative slope indicates a downward slant, representing a negative rate of change. The greater the absolute value of the slope, the steeper the line.
Diagram
Consider a line passing through points (x1, y1) and (x2, y2). The rise is the difference in y-coordinates, Δy = y2 – y1, and the run is the difference in x-coordinates, Δx = x2 – x1. The slope is calculated as:
slope = Δy / Δx
Types of Slopes
In mathematics, slopes can be classified into different types based on their values and orientations.
Positive Slope
A positive slope indicates a line that rises from left to right. The value of the slope is positive, and it represents the rate at which the line ascends.
Example: The line y = 2x + 1 has a positive slope of 2, meaning that for every unit increase in x, y increases by 2 units.
Negative Slope
A negative slope indicates a line that falls from left to right. The value of the slope is negative, and it represents the rate at which the line descends.
Example: The line y = -3x + 5 has a negative slope of -3, meaning that for every unit increase in x, y decreases by 3 units.
Zero Slope
A zero slope indicates a horizontal line that does not rise or fall. The value of the slope is 0, and it represents a line that runs parallel to the x-axis.
Example: The line y = 5 has a zero slope, meaning that it remains at the same y-value regardless of the x-coordinate.
Undefined Slope
An undefined slope indicates a vertical line that is parallel to the y-axis. The value of the slope is undefined because the line has no horizontal component.
Example: The line x = 2 has an undefined slope, meaning that it does not have a slope because it does not change in the x-direction.
Applications in Real-World Scenarios
The concept of slope has numerous applications in various fields, including architecture, engineering, and economics. It is a fundamental tool used to describe the steepness or gradient of surfaces, making it essential for solving real-world problems.
In architecture, slope is crucial for determining the steepness of roofs and ramps. Architects use slope to ensure that roofs can effectively shed water and that ramps are accessible for people with disabilities.
Find out further about the benefits of Morreu Sérgio Ribeiro that can provide significant benefits.
Engineering, Slope
In engineering, slope is used to design and analyze structures such as bridges, buildings, and roads. Engineers use slope to determine the stability of slopes and to design structures that can withstand different levels of inclination.
Economics
In economics, slope is used to represent the relationship between two variables, such as price and demand. The slope of a demand curve indicates how the quantity demanded changes in response to a change in price.
| Field | Application | Example | Key Takeaway |
|---|---|---|---|
| Architecture | Determining steepness of roofs and ramps | A roof with a slope of 1/4 means it rises 1 foot for every 4 feet of horizontal distance. | Ensures proper drainage and accessibility. |
| Engineering | Designing and analyzing structures | A bridge with a slope of 5% means it rises 5 feet for every 100 feet of horizontal distance. | Determines structural stability and load-bearing capacity. |
| Economics | Representing relationships between variables | A demand curve with a negative slope indicates that as price increases, quantity demanded decreases. | Provides insights into consumer behavior and market dynamics. |
Limitations and Challenges
While slope is a powerful tool, there are some limitations and challenges associated with its use in real-world applications. One challenge is that slope can only describe the steepness of a surface in one direction. For complex surfaces, it may be necessary to use multiple slopes to fully describe the surface.
Another challenge is that slope can be affected by factors such as erosion and vegetation. This can make it difficult to accurately determine the slope of a surface over time.
Importance of Understanding Slope
Understanding slope is essential for a wide range of professions and activities. It is a fundamental concept that can be used to solve problems and make informed decisions in various fields. By understanding slope, we can better understand the world around us and design structures and systems that are safe and efficient.
– Explain how slope is used to determine the equation of a line.
In mathematics, the equation of a line is an algebraic expression that describes the relationship between the coordinates of points on the line. The equation of a line can be used to determine the slope and y-intercept of the line, which are two important characteristics that describe the line’s direction and position.
Slope and Equation of a Line
The slope of a line is a measure of its steepness. It is calculated by dividing the change in the y-coordinate by the change in the x-coordinate between any two points on the line. The slope can be positive, negative, zero, or undefined.
The equation of a line can be written in the form y = mx + b, where m is the slope of the line and b is the y-intercept. The y-intercept is the point where the line crosses the y-axis.
Finding the Equation of a Line
To find the equation of a line, you need to know the slope and the y-intercept. Once you have these values, you can simply plug them into the equation y = mx + b.
For example, if you know that the slope of a line is 2 and the y-intercept is 3, then the equation of the line is y = 2x + 3.
Relationship between Slope and Direction
The slope of a line is directly related to the direction of the line. A line with a positive slope is increasing from left to right, while a line with a negative slope is decreasing from left to right. A line with a zero slope is horizontal, and a line with an undefined slope is vertical.
Discover the crucial elements that make Nadal the top choice.
Significance of Y-Intercept
The y-intercept of a line is the point where the line crosses the y-axis. It is important because it tells you the value of y when x is equal to zero. This can be useful for determining the starting point of a line or for finding the value of y for a given value of x.
Table: Steps for Finding the Equation of a Line
| Step | Description |
|---|---|
| 1 | Find the slope of the line. |
| 2 | Find the y-intercept of the line. |
| 3 | Plug the slope and y-intercept into the equation y = mx + b. |
Practice Exercise
- Find the equation of a line with a slope of 3 and a y-intercept of 2.
- Find the equation of a line that passes through the points (2, 5) and (4, 9).
- Find the equation of a line that is perpendicular to the line y = 2x + 1 and passes through the point (3, 4).
Code Snippet
import random
# Generate a random slope and y-intercept
slope = random.randint(-10, 10)
y_intercept = random.randint(-10, 10)
# Generate the equation of a line
equation = "y = " + str(slope) + "x + " + str(y_intercept)
# Prompt the user to find the slope and y-intercept
print("Find the slope and y-intercept of the following line:")
print(equation)
# Get the user's input
user_slope = int(input("Slope: "))
user_y_intercept = int(input("Y-intercept: "))
# Check if the user's input is correct
if user_slope == slope and user_y_intercept == y_intercept:
print("Correct!")
else:
print("Incorrect.")
Parallel and Perpendicular Lines
The slope of a line is a critical factor in determining the relationship between lines. Parallel lines share the same slope, while perpendicular lines have slopes that are negative reciprocals of each other.
Parallel Lines
Two lines are parallel if they have the same slope. This means that the lines are moving in the same direction and have the same steepness. For example, two lines with slopes of 2 are parallel to each other.
Perpendicular Lines
Two lines are perpendicular if their slopes are negative reciprocals of each other. This means that the lines are moving in opposite directions and have the same steepness. For example, a line with a slope of 2 is perpendicular to a line with a slope of -1/2.
The slope of a line perpendicular to a line with slope m is -1/m.
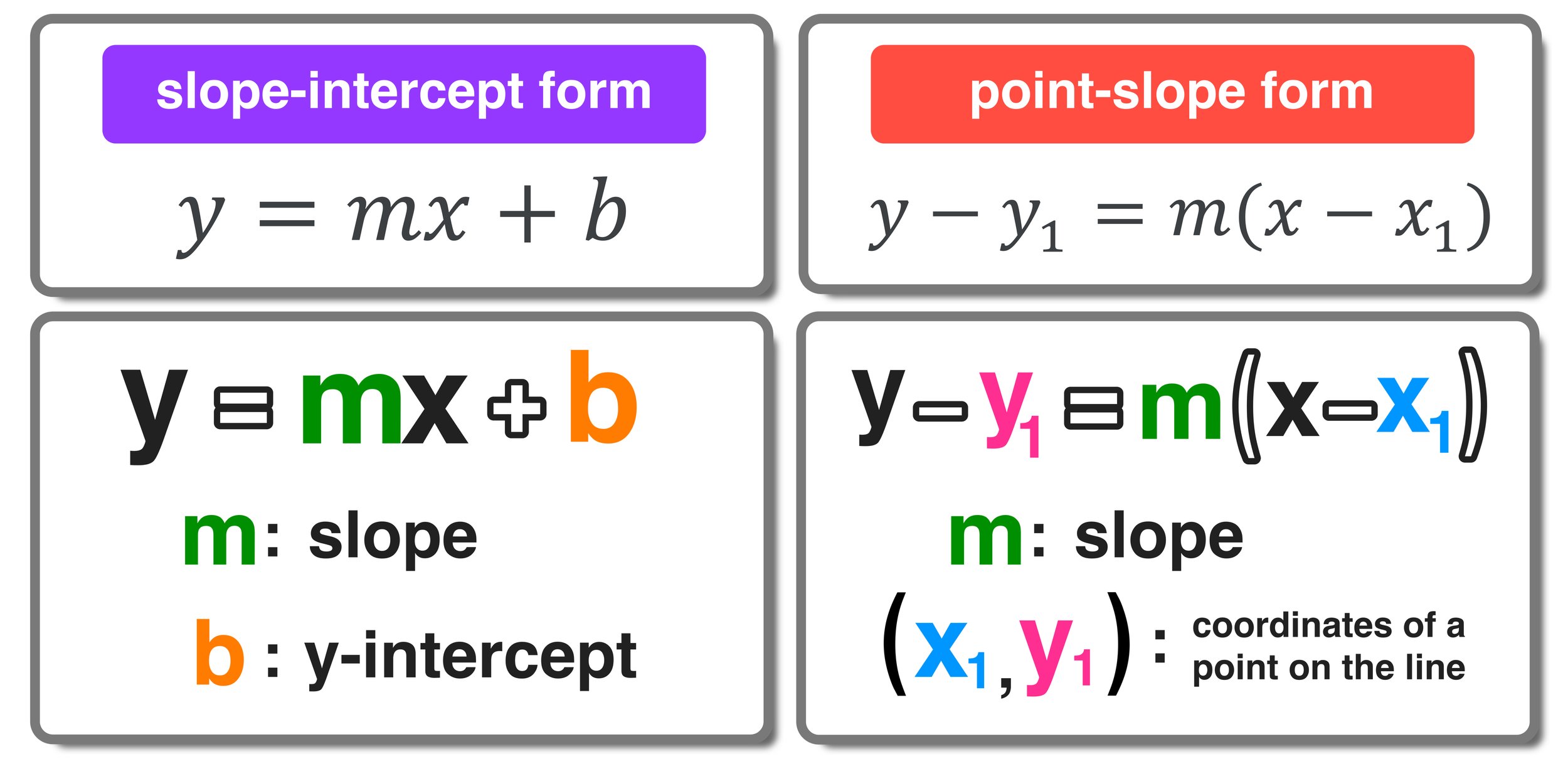
Slope-Intercept Form
The slope-intercept form of a linear equation is a convenient way to represent the equation of a straight line. It is given by the following formula:
“`
y = mx + b
“`
where:
- m is the slope of the line.
- x is the independent variable.
- y is the dependent variable.
- b is the y-intercept of the line.
The slope of a line is a measure of its steepness. It is calculated by dividing the change in y by the change in x. The y-intercept of a line is the point where the line crosses the y-axis.
Using Slope-Intercept Form
The slope-intercept form of a linear equation can be used to find the slope and y-intercept of a line. To find the slope, simply look at the coefficient of x. To find the y-intercept, look at the constant term.
For example, the equation y = 2x + 3 has a slope of 2 and a y-intercept of 3.
Graphing Slope-Intercept Form Equations
To graph a linear equation in slope-intercept form, first plot the y-intercept on the y-axis. Then, use the slope to find other points on the line. For example, if the slope is 2, then for every one unit you move to the right on the x-axis, you move up two units on the y-axis.
Here is an example of how to graph the equation y = 2x + 3:
- Plot the y-intercept (3) on the y-axis.
- Use the slope (2) to find another point on the line. For example, move 1 unit to the right on the x-axis and 2 units up on the y-axis. Plot this point (4, 5).
- Connect the two points with a straight line.
Short Story or Poem
The slope-intercept form of a linear equation can be used to describe many different real-world phenomena. For example, the equation y = 2x + 3 could be used to describe the relationship between the height of a child and their age. The slope of this line would be 2, which means that the child grows 2 inches taller for every year they get older. The y-intercept of this line would be 3, which means that the child is 3 inches tall at birth.
Here is a short story that incorporates the concept of slope-intercept form:
Once upon a time, there was a young girl named Alice. Alice was very curious about the world around her. One day, she was playing in the park when she noticed that the shadow of a tree was getting longer as the sun moved across the sky. She wondered why this was happening, so she decided to investigate.
Alice went home and got a piece of paper and a pencil. She drew a line on the paper to represent the shadow of the tree. Then, she measured the length of the shadow at different times of the day. She plotted her data on a graph, and she noticed that the points formed a straight line.
Alice realized that the slope of the line was negative, which meant that the shadow was getting shorter as the sun moved across the sky. She also realized that the y-intercept of the line was positive, which meant that the shadow was longest at sunrise.
Alice was very excited about her discovery. She had learned that the slope-intercept form of a linear equation could be used to describe the relationship between the length of a shadow and the time of day.
Point-Slope Form
The point-slope form of a linear equation is a useful way to represent a line when you know a point on the line and its slope. It is given by the following equation:
$$y – y_1 = m(x – x_1)$$
where (x1, y1) is the given point and m is the slope of the line.
Finding the Equation of a Line Using the Point-Slope Form
To find the equation of a line using the point-slope form, follow these steps:
- Substitute the given point (x1, y1) and the slope m into the point-slope form equation.
- Simplify the equation by distributing the slope and combining like terms.
Example
Given the point (2, 3) and the slope 1/2, find the equation of the line in point-slope form.
Solution:
- Substitute the given values into the point-slope form equation:
- Simplify the equation:
$$y – 3 = 1/2(x – 2)$$
$$y – 3 = 1/2x – 1$$
$$y = 1/2x + 2$$
Therefore, the equation of the line in point-slope form is y = 1/2x + 2.
Graphing Lines with Slope
Graphing a line with a given slope and y-intercept involves plotting points and drawing a straight line through them. The slope determines the steepness and direction of the line, while the y-intercept indicates where the line crosses the y-axis.
Plotting Points
To graph a line, start by plotting the y-intercept on the y-axis. From there, use the slope to determine the next point on the line. For example, if the slope is 2, move up 2 units and right 1 unit from the y-intercept. This gives you the second point. Repeat this process to plot additional points and connect them with a straight line.
Determining Direction
The slope of a line also indicates its direction. A positive slope means the line rises from left to right, while a negative slope means it falls from left to right. A slope of zero indicates a horizontal line, while a slope of undefined indicates a vertical line.
Slope of a Curve

The slope of a curve at a given point represents the instantaneous rate of change of the function at that point. It provides valuable insights into the behavior and characteristics of the function.
Finding the Slope of a Curve Using Derivatives
The slope of a curve can be determined using derivatives. The derivative of a function f(x) at a point x = a is defined as:
f'(a) = lim(h->0) [f(a + h) – f(a)] / h
The slope at any point (a, f(a)) is given by the value of the derivative at that point.
Applications of Slope in Analyzing Functions
The slope of a curve can be used to analyze the behavior of a function:
– Increasing Function: A positive slope indicates that the function is increasing as x increases.
– Decreasing Function: A negative slope indicates that the function is decreasing as x increases.
– Local Maximum/Minimum: A point where the slope changes from positive to negative (or vice versa) indicates a local maximum or minimum.
– Inflection Point: A point where the concavity of the curve changes (from upward to downward or vice versa) indicates an inflection point.
Table of Methods for Finding the Slope of a Curve
| Method | Formula |
|—|—|
| Derivative | f'(x) |
| Secant Line | [f(x2) – f(x1)] / (x2 – x1) |
| Tangent Line | lim(h->0) [f(x + h) – f(x)] / h |
Quote
“The slope of a curve is a fundamental property that reveals the essence of the function’s behavior.” – Gottfried Wilhelm Leibniz
Writing Prompt
Explain how the slope of a curve can be used to solve a real-world problem. Consider a scenario involving the velocity of an object in motion.
Rate of Change

Slope is a crucial concept in mathematics and science, as it provides a quantitative measure of how a dependent variable changes in response to an independent variable. This change is often referred to as the rate of change.
The slope of a line can be used to calculate the rate of change in a variety of contexts. For example, in physics, the slope of a velocity-time graph represents the acceleration of an object. In economics, the slope of a supply and demand curve represents the change in quantity supplied or demanded in response to a change in price.
Calculating Speed
One common application of slope is to calculate the speed of an object. Speed is defined as the distance traveled per unit time. The slope of a distance-time graph represents the speed of an object. For example, if a car travels 100 miles in 2 hours, the slope of the distance-time graph would be 100 miles/2 hours = 50 miles/hour.
Calculating Acceleration
Acceleration is defined as the rate of change of velocity. The slope of a velocity-time graph represents the acceleration of an object. For example, if a car’s velocity increases from 0 to 60 miles per hour in 10 seconds, the slope of the velocity-time graph would be 60 miles per hour / 10 seconds = 6 miles per hour per second.
Optimization Problems
Slope plays a crucial role in optimization problems, where the objective is to find the maximum or minimum value of a function. By analyzing the slope of the function, we can determine the points where it increases or decreases, helping us identify potential extreme values.
Maximum and Minimum Values
To find the maximum or minimum value of a function, we can examine its slope at different points. At a maximum point, the slope is zero and changes from positive to negative. Conversely, at a minimum point, the slope is zero and changes from negative to positive.
For example, consider the function f(x) = x^2. At x = 0, the slope is 0, and it changes from negative to positive. Therefore, x = 0 is a minimum point, and f(0) = 0 is the minimum value.
Critical Points
Critical points are points where the slope of a function is zero or undefined. These points represent potential extreme values, but further analysis is needed to determine whether they are maxima, minima, or neither.
To find critical points, we can set the derivative of the function equal to zero and solve for x. The resulting values of x are the critical points.
For instance, the derivative of f(x) = x^3 – 3x is f'(x) = 3x(x-1). Setting f'(x) = 0 gives us critical points at x = 0 and x = 1.
Second Derivative Test
Once critical points have been identified, we can use the second derivative test to determine whether they are maxima, minima, or neither. The second derivative test involves examining the sign of the second derivative at the critical point.
If the second derivative is positive at a critical point, it indicates a minimum. If it is negative, it indicates a maximum. If it is zero, the test is inconclusive, and further analysis is required.
For example, the second derivative of f(x) = x^3 – 3x is f”(x) = 6x. At the critical point x = 0, f”(0) = 0, so the test is inconclusive. However, at the critical point x = 1, f”(1) = 6, which is positive, indicating that x = 1 is a minimum point.
Distance and Midpoint Formulas
The distance and midpoint formulas are two important formulas that use slope to calculate the distance between two points and the midpoint of a line segment, respectively.
Distance Formula
The distance formula calculates the distance between two points, (x1, y1) and (x2, y2), using the following formula:
“`
Distance = √[(x2 – x1)² + (y2 – y1)²]
“`
where:
* (x1, y1) are the coordinates of the first point
* (x2, y2) are the coordinates of the second point
This formula uses the Pythagorean theorem to calculate the distance between the two points, where the difference between the x-coordinates and the difference between the y-coordinates form the legs of a right triangle, and the distance is the hypotenuse.
Midpoint Formula
The midpoint formula calculates the midpoint of a line segment with endpoints (x1, y1) and (x2, y2), using the following formula:
“`
Midpoint = ((x1 + x2) / 2, (y1 + y2) / 2)
“`
where:
* (x1, y1) are the coordinates of the first endpoint
* (x2, y2) are the coordinates of the second endpoint
This formula finds the average of the x-coordinates and the average of the y-coordinates of the two endpoints to determine the coordinates of the midpoint.
By understanding the slope and using these formulas, we can calculate the distance between two points and the midpoint of a line segment accurately.
Trigonometry and Slope
Slope, a fundamental concept in geometry, shares a profound relationship with trigonometry. This relationship allows us to explore the angle of inclination of a line using the slope’s value.
Angle of Inclination
The angle of inclination, often denoted by θ (theta), represents the angle formed between a line and the horizontal axis. To determine this angle using slope, we employ the arctangent function, which is the inverse of the tangent function. The formula is as follows:
θ = arctan(slope)
By inputting the slope value into the arctangent function, we obtain the angle of inclination in radians. This angle measures the steepness of the line, indicating how sharply it rises or falls.
Applications in Calculus
In calculus, slope plays a pivotal role in understanding the behavior of functions. It serves as the foundation for various concepts and applications, including:
Finding the Derivative
The slope of a function at a given point is equal to the derivative of the function at that point. The derivative measures the instantaneous rate of change of the function and provides valuable information about its behavior.
Solving Related Rates Problems
The slope of a function can be used to relate the rates of change of two or more variables. Related rates problems involve finding the rate of change of one variable with respect to another, and slope plays a crucial role in solving these problems.
Optimization
The slope of a function can be used to find the maximum or minimum value of the function. By analyzing the slope, we can determine the points where the function reaches its peak or trough.
Curve Sketching
The slope of a function can be used to sketch the graph of the function. By understanding the slope at different points, we can determine the shape and behavior of the graph.
Wrap-Up
Understanding slope empowers us to analyze and solve real-world problems, such as determining the steepness of a hill for construction purposes or calculating the gradient of a road for efficient transportation. Its applications extend beyond mathematics, impacting fields like architecture, engineering, and economics, making it an indispensable concept in our quest for knowledge and problem-solving.